Favard operator
In functional analysis, a branch of mathematics, the Favard operators are defined by:
where 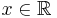 ,
, 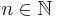 , and
, and 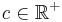 .[1] They are named after Jean Favard.
.[1] They are named after Jean Favard.
Generalizations
A common generalization is:
where 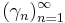 is a positive sequence that converges to 0.[1] This reduces to the classical Favard operators when
is a positive sequence that converges to 0.[1] This reduces to the classical Favard operators when 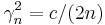 .
.
References
- Favard, Jean (1944). "Sur les multiplicateurs d'interpolation". Journal de Mathematiques Pures et Appliquees 23 (9): 219–247. (French) This paper also discussed Szász–Mirakyan operators, which is why Favard is sometimes credited with their development (eg Favard–Szász operators).
Footnotes
- ^ a b Nowak, Grzegorz; Aneta Sikorska-Nowak (14 November 2007). "On the generalized Favard–Kantorovich and Favard–Durrmeyer operators in exponential function spaces". Journal of Inequalities and Applications 2007: 1. doi:10.1155/2007/75142. http://www.hindawi.com/journals/jia/raa.75142.html.
 = \frac{\sqrt{n}}{n\sqrt{c\pi}} \sum_{k=-\infty}^\infty {\exp{\left({\frac{-n}{c} {\left({\frac{k}{n}-x}\right)}^2 }\right)} f\left(\frac{k}{n}\right)}](/2012-wikipedia_en_all_nopic_01_2012/I/cb99d34e0781607db416dfe657a2b390.png)
 = \frac{1}{n\gamma_n\sqrt{2\pi}} \sum_{k=-\infty}^\infty {\exp{\left({\frac{-1}{2\gamma_n^2} {\left({\frac{k}{n}-x}\right)}^2 }\right)} f\left(\frac{k}{n}\right)}](/2012-wikipedia_en_all_nopic_01_2012/I/33e7e862504948963b6a888f02fa9fd8.png)